آزمون كلموگروف-اسميرونوف به عنوان يک آزمون تطابق توزيع برای داده های کمی است. فرض کنيد نمونه ای از انداره های کمی در اختيار دارید و می خواهید تعيين کنید که آيا اين نمونه از جامعه ای با توزيع نرمال بدست آمده است يا خير؟ آزمون نرمال بودن يک توزيع يکی از شايع ترين آزمون ها برای نمونه های کوچک است که محقق به نرمال بودن آن شک دارد. برای اين هدف آزمون آزمون كلموگروف-اسميرونوف آزمون مناسبی است.
در نرم افزار SPSS از آزمون كلموگروف-اسميرونوف برای تطابق چهار توزيع مختلف نرمال، پواسن، نمايی و يکنواخت استفاده شده است. اساس آزمون كلموگروف-اسميرونوف روش بر اختلاف بين فراوانی تجمعی نسبی مشاهدات با مقدار مورد انتظار تحت فرض صفر است. فرض صفر می گويد که نمونه انتخاب شده دارای توزيع نرمال، (پواسن، نمايی يا يکنواخت) است. آزمون کلموگروف–اسميرونوف برای تطابق توزيع، احتمال های تجمعی مقادير در مجموعه داده هايتان را با احتمال های تجمعی همان مقادير در يک توزيع نظری خاص مقايسه می کند. اگر اختلاف آن به قدر کافی بزرگ باشد، كلموگروف-اسميرونوف نشان خواهد داد که داده های شما با يکی از توزيع های نظری مورد نظر تطابق ندارد. در آزمون كلموگروف-اسميرونوف اگر معيار تصميم گیری P-Value کمتر از 5 درصد باشد، فرض صفر رد می شود يعنی داده ها نمی توانند از يک توزيع خاص مانند نرمال، پواسن، نمايی يا يکنواخت باشند. برای درک بهتر اين آزمون به يک مثال عملی که با نرم افزار SPSS انجام شده است توجه کنيد.
فرض کنید می خواهیم داده های بارش منطقه ای را بررسی کنیم ببینیم تا این داده ها دارای توزیع نرمال هستند یا خیر (گرچه می دانیم داده های بارش از تابع نرمال پیروی نمی کنند).
برای بررسی اينکه آيا داده ها از يک توزيع نرمال به دست آمده اند يا خير، از آزمون كلموگروف-اسميرونوف استفاده می کنیم.
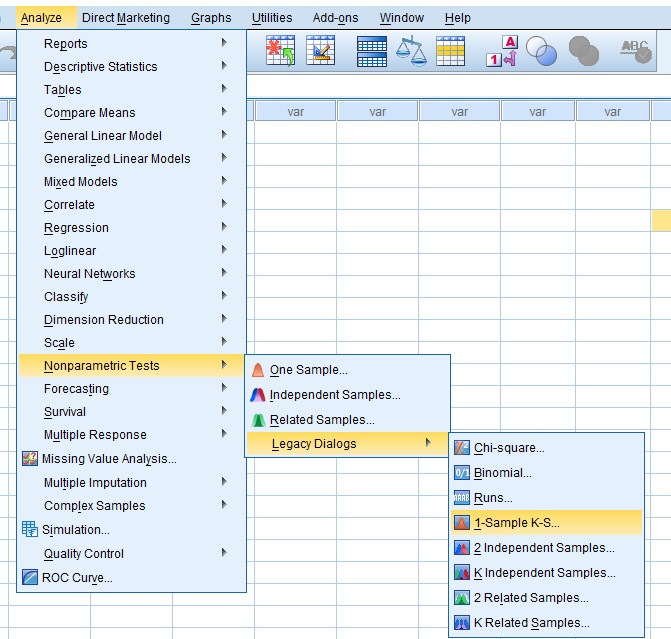
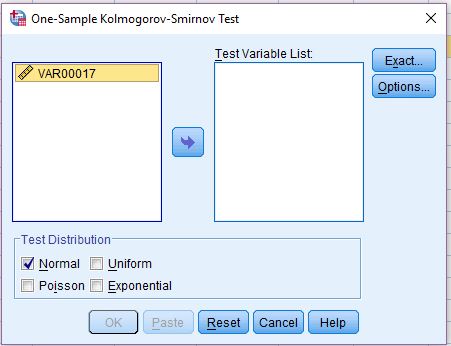
در شکل زیر محل قرار گیری كلموگروف-اسميرونوف در SPSS نشان داده شده است.
در یک ستون داده های بارش را وارد کنید و سپس مانند شکل زیر آن را انتخاب و تابع نرمال را تیک بزنید. داده ها باید با استفاده از آیکون موجود در وسط به قسمت Test variable list بروند
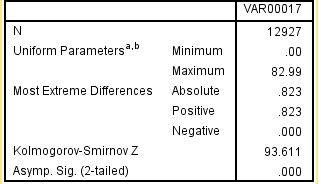
با توجه به نتیجه که در آخرین سطر آمده است (2-tailed) می توان دریافت که از تابع نرمال پیروی نمی کند.
این آزمون را برای داده های دما، رواناب و سایر متغییرهای اقلیمی تست کنید و نتیجه را با هم مقایسه کنید.